Deep learning is an artificial intelligence (AI) function that imitates the workings of the human brain in processing data and creating patterns for use in decision making. It has achieved success in many fields. We have done some works about development and application of deep learning technique including (but not confining to)
1. Develop a new deep neural network for fast reconstruction of non-uniform sampling signal
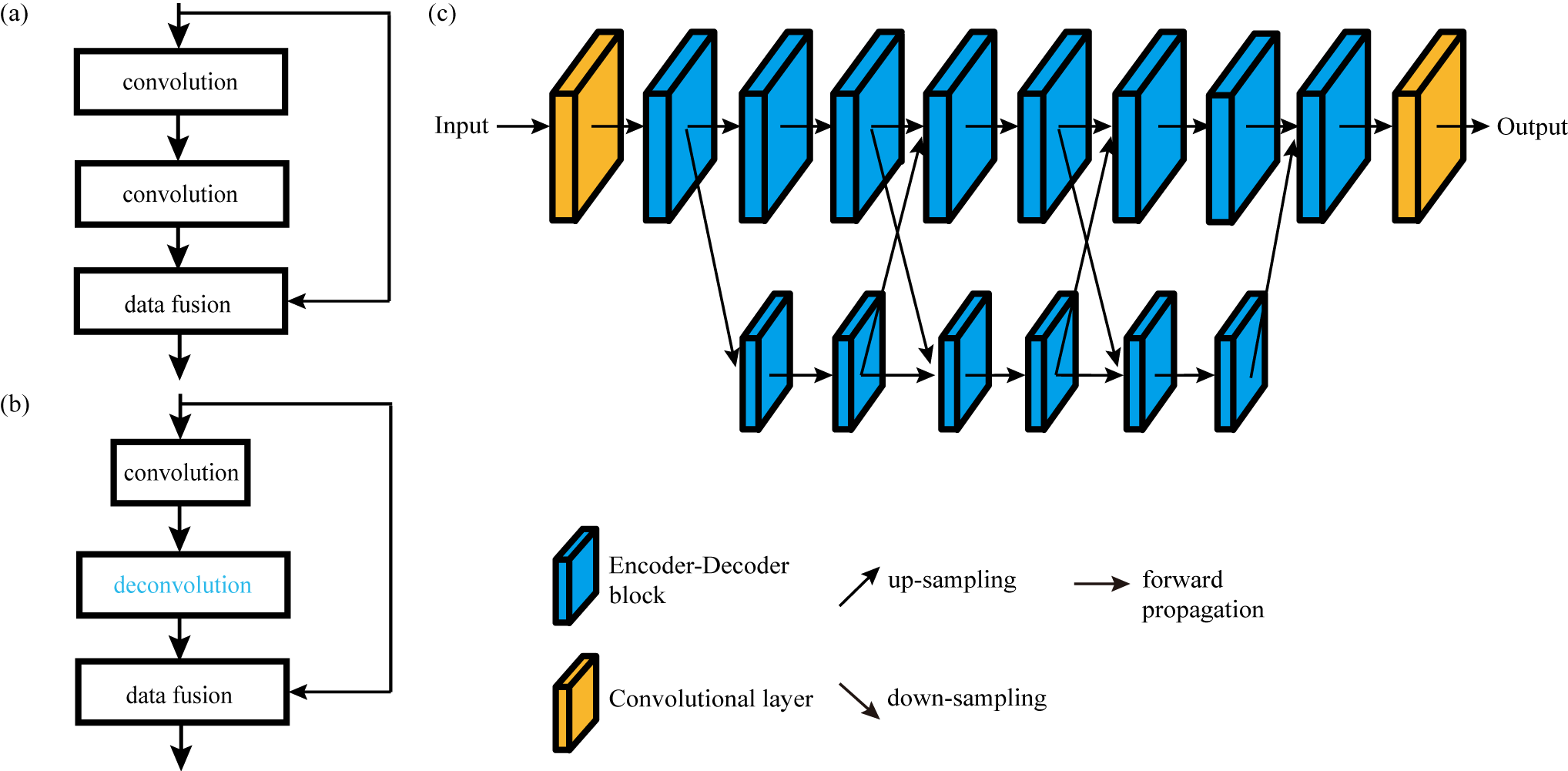
Figure 1. (a) Residual learning block. (b) Encoder-Decoder (ED) learning block. The convolution layer is an encoder that reduces data dimensionality, and the deconvolution layer (blue) is a decoder that recovers data dimensionality. (c) The proposed EDHRN which is based on HRNet. It consists two parallel subnetworks. The upper subnetwork contains ED blocks and convolutional layers, and the lower subnetwork is formed only by ED blocks. There are repeated connections between the two subnetworks by down-sampling and up-sampling.
A deep Encoder-Decoder High-Resolution Networks (EDHRN) is proposed. The structure of EDHRN is based on High-Resolution Net (HRNet) which was proposed for human pose estimation. The architecture of EDHRN is illustrated in Fig. 1(c). The most prominent difference between EDHRN and other typical CNNs (e.g. DenseNet) is that EDHRN has a unique structure of parallel subnetworks. It is noted that the recovery of weak peaks from NUS data is a vital issue for NMR spectral reconstruction. Since HRNet has an excellent ability to preserve the image details, the main structure of HRNet, i.e., the structure of parallel subnetworks, is kept in EDHRN to preserve the weak peaks (counterpart of the image details) in NMR spectra. A general operation in NMR spectral reconstruction is to fill undersampled FID data with zeros on non-acquired positions, but this leads to strong artifacts. Thus, a functional block called Encoder-Decoder (ED) block (Fig. 1(b)) is introduced into the EDHRN to replace the residual block (Fig 1(a)) in original HRNet. The concept of ED structure was proposed for the reduction of data dimensionality, but it has already been shown that ED structure is also effective for removing artifacts, image denoising, image reconstruction, etc. Here, we utilise ED blocks to improve artifact removal.
2. Develop a new deep neural network for suppressing noise
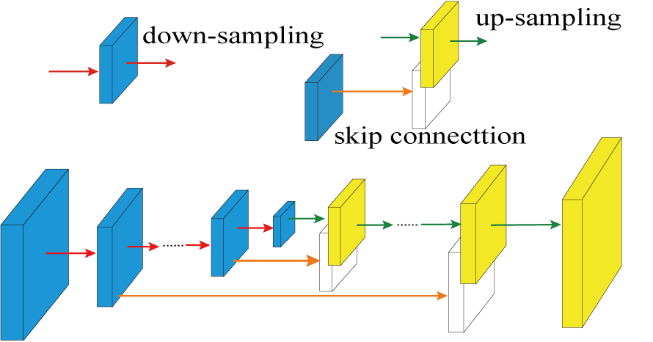
Figure 2. The overall architecture of DN-Unet including down-sampling, up-sampling, and skip connection. The red, green, and orange arrows show the down-sampling operations for shrinking the size, the up-sampling operations for recovering the size and the skip connections for retaining spectral details lost during down-sampling, respectively.
The architecture of the proposed DN-Unet is shown in Figure 2. It is based on a classical convolutional neural network (CNN), Unet, which was utilized for biomedical image segmentation. The proposed network consists of convolutional and deconvolutional layers. Convolutional layers implement down-sampling operations while deconvolutional layers implement up-sampling operations. The combination of down-sampling and up-sampling is a typical structure called encoder-decoder (ED). The ED structure is widely used in the field of image denoising. Similarly, CNN demonstrated an excellent performance for image denoising. Therefore, we propose DN-Unet combining ED and CNN for NMR spectra denoising based on the fact that NMR spectra can be treated as a kind of image. However, spectral details (e.g. weak peaks) may lose after down-sampling operations. Thus, skip connections are introduced into the proposed network. The convolutional layers are directly connected to corresponding deconvolutional layers to retain spectral details in the output of deconvolutional layers.
It should be noted that multiple noisy spectra (i.e. inputs) correspond to a same single noiseless spectrum (i.e., label) (M-to-S) in the training data set. This is different from the routine DL strategy that a single input corresponds to a single label (S-to-S). M-to-S strategy produces higher SNR and lower MSE (mean square error) than S-to-S strategy, suggesting better denoising and more accurate spectral reconstruction. 1D spectra were used to train 1D model. This model can be used to denoising not only 1D spectra but also 2D spectra in a way of line by line along the direct dimension. 2D model using 2D training spectra can also be trained to denoising 2D spectra. However, 1D model requires less training time, has less requirement on disk space, especially on graphics memory, and obtains denoised spectra with lower MSEs, indicating more accurate results.

