信号与谱图处理对于改善信号和谱图的质量可以起到重要的作用,我们进行下列(但不限于)的工作:
1. 对纯化学位移谱进行拉东变换获取化学位移变化信息
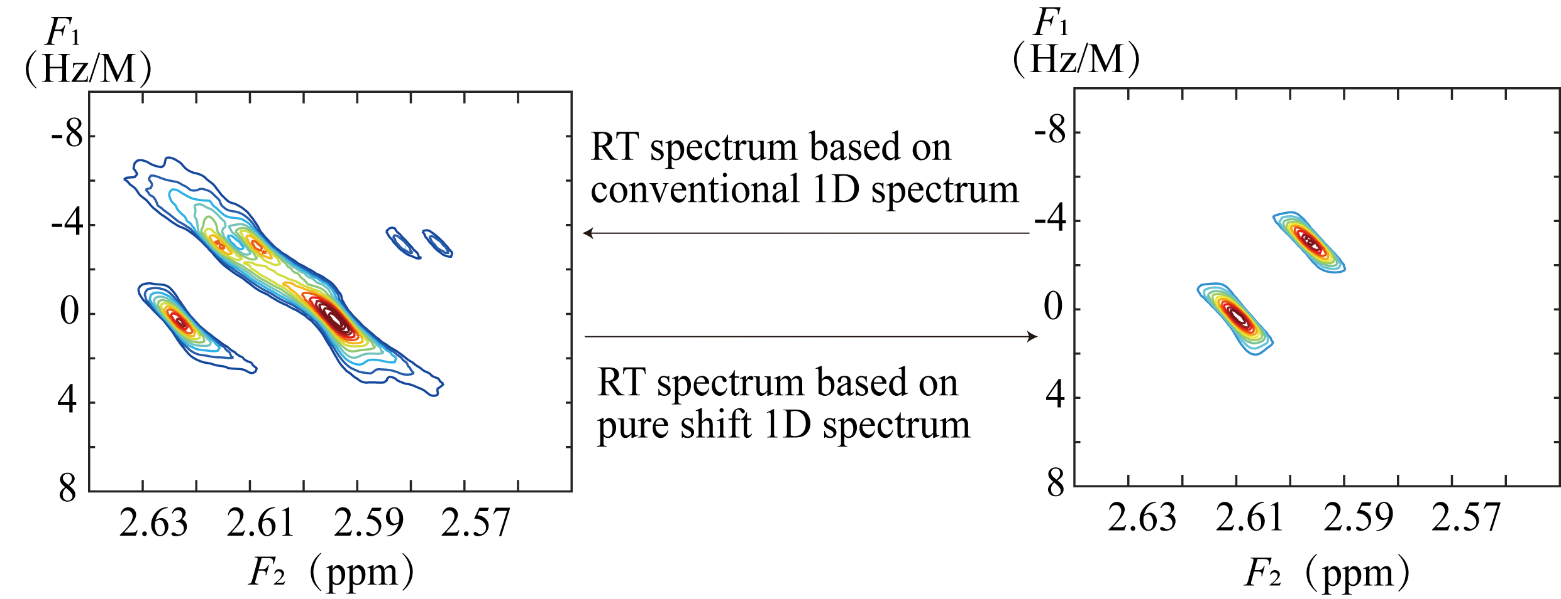
物质的化学位移会因为温度、pH值、溶质等因素的变化而发生特定的变化,这种变化在研究物质性质与化学结构时有重要意义。常用的傅里叶变换无法对这种线性变换过程继续处理,而逐个谱峰进行数值拟合分析获取谱峰的化学位移偏移率的方法所需计算量与谱峰个数相关,效率低下,同时,所得到的结果缺乏直观性,且当谱图中,出现谱峰混叠时,由于谱峰混叠的谱峰相互干扰,致使单纯的数值拟合分析方法无法继续进行。此时,对这种线性变化关系的分析,引入拉东变换技术。根据拉东变换的特性,其能将特定直线上的积分结果投影到变换空间,实现对于线性关系的分析。因此,利用拉东变换分析谱峰顺序排列后的数据,将各个谱峰的偏移速度投影至变换空间,即构成了基于拉东变换的二维谱。该二维谱直接维显示信号的化学位移信息,间接维为化学位移偏移率,这样就可以直接读取二维谱图就能得到各个谱峰信号的偏移率。
2. 基于近似l0范数最小化的谱图稀疏重建算法
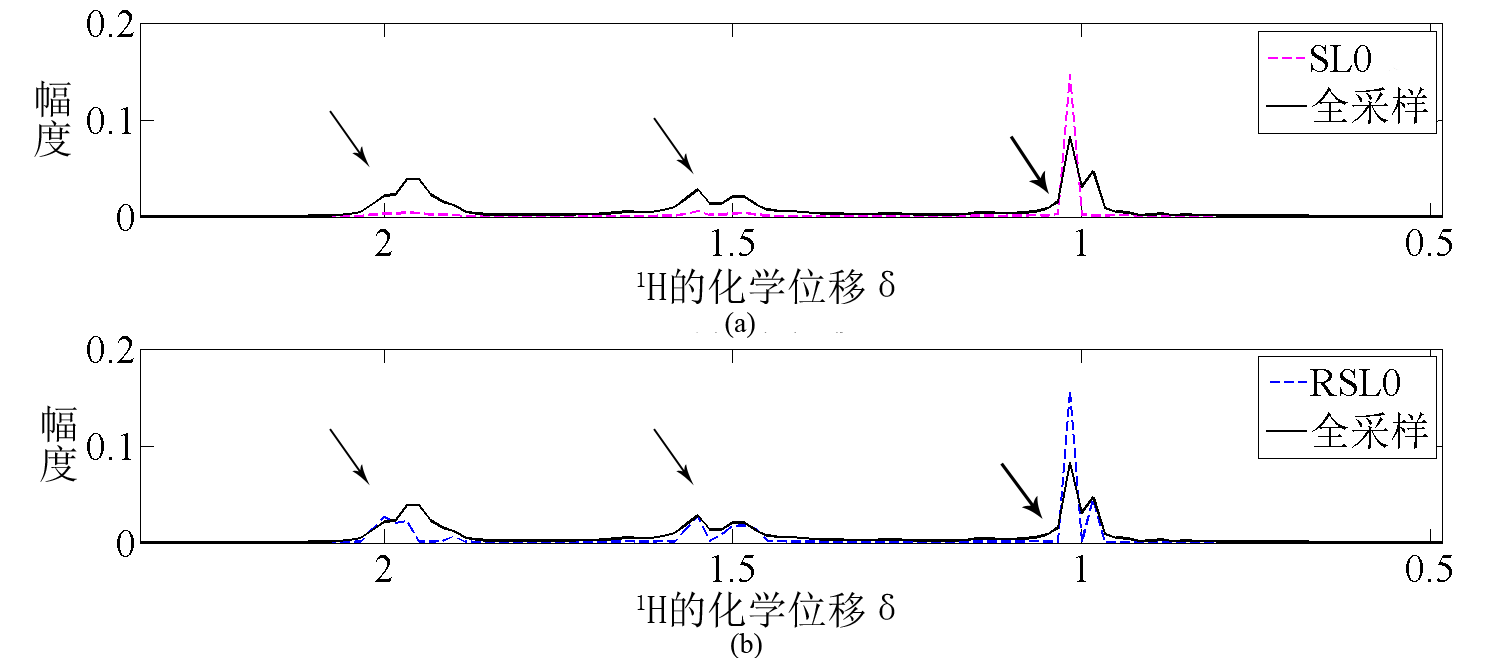
(a)为SL0法与全采样对比图,(b)为RSL0法与全采样对比图
过长的数据采集时间会使很多高分辨率多维谱应用难以实现。传统的解决办法是使用随机非均匀采样代替奈奎斯特采样,但这样会使谱图质量受损。压缩传感的出现为此提供了更好的解决办法,合适的压缩传感重建算法可以通过很少的随机非均匀采样将谱图高质量的重建出来。提出了“迭代重复加权平滑l0范数最小化”算法(Re-weighted smoothed l0 norm Minimization,RSL0),主要通过运用迭代重复加权技术来解决噪声大小与重建精度之间的矛盾,同时在最优化算法上使用定点迭代法代替梯度下降法,减少了运算时间,使其更适用于大规模数据的重建。
3. 通过采用32通道的阵列线圈改善信噪比

当体素中心位于不同位置时32通道线圈和CP头线圈之间的SNR比率。矩形代表体素中心(中间的那个矩形和磁体中心重合),矩形中的数值代表SNR比率(三次重复测量的平均值)。
对于采用阵列线圈的实验,先由陈列线圈的每个元素线圈采得谱图信号,然后将这些谱图合并为一张谱图。因此,高效的组合算法是很关键的。在组合谱图过程中重要的步骤是确定权重因子。我们采用多通道非参数的奇异值分解法(Singular Value Decomposition, SVD),它使用所有的fid数据点估计权重因子。

